Header image: KF in Dall-E

I have been fascinated by Möbius strips for several years now. It began in a Teacher Inquiry class where we were using a textbook called Spirals of Inquiry. At the time, I mentioned to the instructor that the image of a spiral of inquiry didn’t sit right with me as, by definition, one moves further away from the centre as the spiral grows. It seems that there should be a return to the centre, the starting point, for the inquiry to be of value.

However, representing this return as a cycle of inquiry forgoes the visual representation of a change in point of view or understanding. To me, a cycle seems somewhat procedural: a clinical, simple sequence of steps a person might follow, even with their eyes and mind closed, completing the cycle without it having had any impact or effect whatsoever.
To add: Lacan and His Möbius Strip
https://chroma.mit.edu/p/lacan-and-his-mobius-strip
- Locally, at any single point, we can see a distinct inner and outer side, suggesting a clear conflicting relationship. But globally, if we look at the entire model, we cannot see where one side turns to the other side; here the opposition only proves the inseparability between the two opposites.
Concepts
I then came upon the Möbius strip which immediately appealed to me as a helpful tool for conceptualizing any number of ideas. After outlining a few background concepts in a simplified way (the only way I can understand them for now!), I will attempt to explain the utility of the Möbius strip.
Dimensions
A line is a 1-dimensional shape, having length only. If you put two dots on a flat piece of paper, you can imagine the line that joins them. When you actually draw that line with a pencil, it is merely a representation of a line because it has become 2-dimensional: the width of the line, however narrowly you draw it, adds this dimension.
- If you think about it, a line drawn on a piece of paper is really a long rectangle with a teeny tiny width. Thus, a “true line” is one that is imagined as that line that joins two dots, like the ones below.

Now, a “true Möbius strip” also has two dimensions, having length and width. Similar to a line, this can only be imagined: making a Möbius strip out of paper adds a third dimension – the height (thickness) of the paper. As with a line, no matter how fine the paper is, the strip of paper is still essentially a cuboid (think shoebox) that is long, wide, but of tiny height: imagine the verticals below, e.g. A-F, as 0.01mm
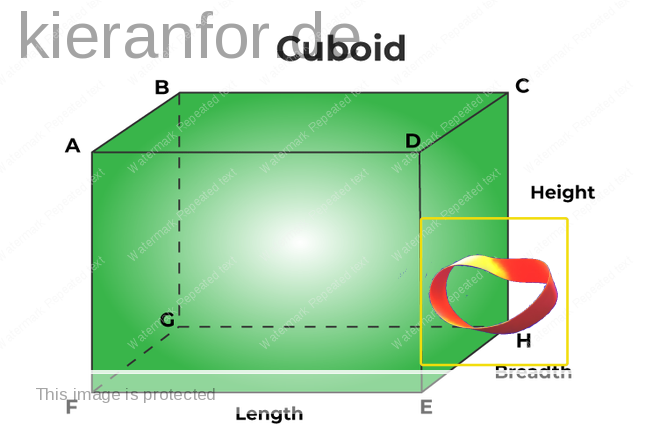
Of course, we could represent a line/Möbius strip on a screen but even these representations will have a pixel measurement, however small, that renders the former 2-dimensional and the latter 3-dimensional.
➡ For consideration of how 4-dimensional space can be represented in 3-dimensional space, see the Klein Bottle and the Tesseract.

The long and the short of it is, when we make Möbius strips out of a piece of paper, it is merely a representation of a Möbius strip. I mention this as I need to distinguish between the use of Möbius strips as conceptual tools for duality, triality, and quadrality.
Topology
“A topologist studies properties of objects that are preserved when moved, bent, stretched or twisted, without cutting or gluing parts together.” [1]
I get lost almost immediately in the math of topology, especially in the discussion of holes (Though this is easier and more fun to follow). One concept, however, is essential to understand to make sense of Möbius strips: orientability.
- Imagine you write a message on a transparent glass loop; You then walk around the loop, back to where you started. You look down and you can easily read what you wrote. A loop is orientable.

(and not an opaque Ancient Roman glass bangle!)
- Now, Imagine you write a message on a transparent glass Möbius strip. You walk around the strip until you see the message under your feet. The message appears as a mirror image. You are back where you started (remember the loop has no thickness) but your point of view is different: A Möbius strip is non-orientable.
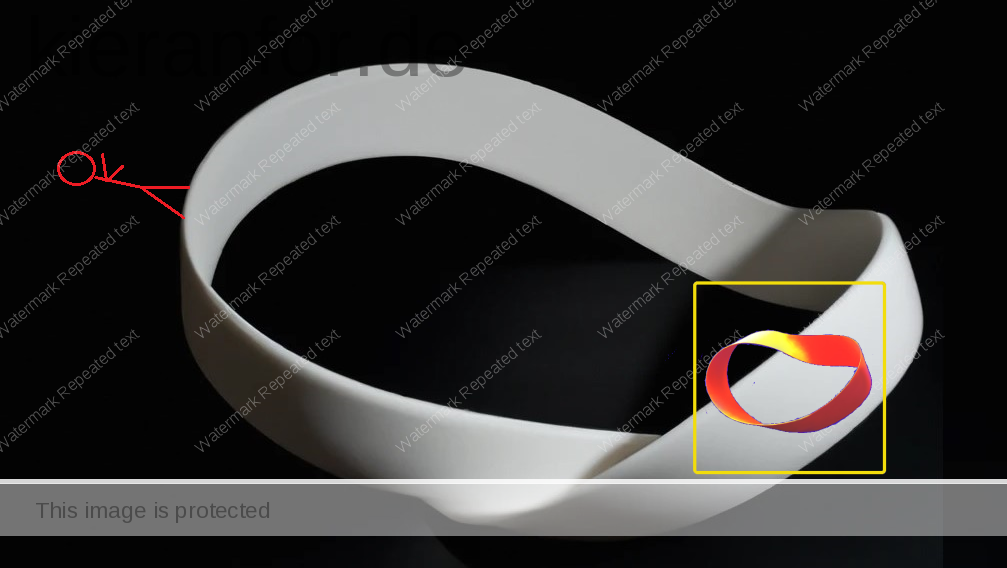
but on the other “side”
Edges and sides/faces.
- A square has four edges and NO faces/sides: it is 2-dimensional.
- A square is simply four straight lines connecting at right angles and, as we know, lines are 1-dimensional. As such, a square has length and width, but no height.
- A cube, in contrast, has 12 edges and six faces, each with two sides; it is 3-dimensional: A cube has an “inside”: a square has no sides at all.
You place a square book on a table. The book is in contact with the table; there is nothing between the book and the table (at least in theory). This nothing is something. It is a 2-dimensional space that has length and width and no thickness. It is an actual square. This square had two sides. It has an adjacent area were the book is and an adjacent area were the table is. If you are going to shade one side of this square, you are going to shade either the book or the table. If you want to shade the square itself there is nothing to shade. There is nothing you can draw on, or paint on. Remember this square has no thickness; you can’t divide it through its thickness into two squares; so even if you could somehow shade a square, you can’t do it selectively, it’s all or nothing.
user756887 on Math Substack
Möbius Strip V cycle/spiral
My original attraction to the Möbius strip was due to its non-orientability. As I mentioned, a cycle seems to lack the idea of transformation/wonder. In contrast, when one engages with a Möbius strip and proceeds through inquiry/learning/exploration, one inevitably finds oneself back at the point of origin but at the other “side”. The person has been reoriented; the journey has changed their perspective.
- This seems really impactful to me but I don’t know if others will find it so. It represents, for example, the potential for inquiry to allow us to see our practices from a different point of view. Continuing along the strip, one returns to the actual point of origin having been reoriented through the process. Continuing along, given the lack of boundaries, one could engage in ongoing (potentially infinite) reorientation.
Duality
This one is easy to follow. Some things are/should be/can be/must be two things at the same time. A Möbius strip can represent this easily.


In The Unaddressed “I” of Ideology Critique, Pinar quotes Butler:
Power not only acts on a subject but, in a transitive sense, enacts the subject into being. As a condition, power precedes the subject. Power loses its appearance of priority, however, when it is wielded by the subject, a situation that gives rise to the reverse perspective that power is the effect of the subject, and that power is what the subject effects.
and then remarks
Simultaneously interpellated and self-constituting, the subject acts after— and in the midst of— being acted upon.
The image above helps me to, literally, picture this. It’s also helpful to envision more evident relationships




Could we say the same for a math teacher; are they mathematicians & teachers? Or are they teachers who teach math?
What of a chef education teacher?
⬇
Maxwell, B. (2018). When Teachers’ Off-Duty Creative Pursuits Conflict with Role Model Expectations: A Critical Analysis of Shewan. Interchange, 49(2), 161–178. https://doi.org/10.1007/s10780-018-9320-y

Shulman (1997): “Teaching is a dual act of intelligence and empathy. It entails both technical and moral reason.”


ﻼF: Personal inquiry precedes, coincides with, and succeeds professional inquiry
Cutting
- A Möbius strip has only one side; you can establish this by drawing a line down the centre, along the length. You will find your line meets itself without you ever having lifted the pen.
- When you cut the Möbius strip down the middle, the result is a boring loop with two twists.
- No fun!
- BUT, If you cut the strip at the one-third point, and keep going all the way around….


- …you produce a conjoined Möbius strip AND a loop with two twists (twice as long as the Möbius strip)

- This Möbius strip is smaller than the original because you have cut it out of the centre of the original Möbius strip and, by doing so, produced the double twisted loop.
- This was relevant for me; a perfect metaphor for inquiry. The double twisted loop represents the learning generated from journeying around the Möbius strip.
- Through reorientation, new perspectives have been realized and generated while the Möbius strip remains in place ready for another circuit, cutting at the one-third point, where this generative property can be realized, potentially an infinite number of times.
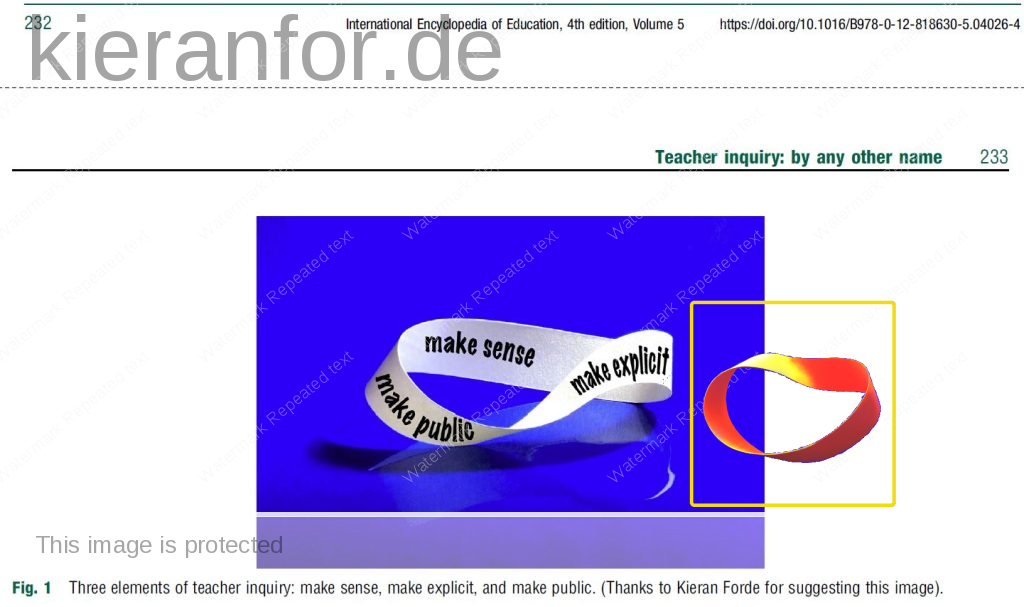
Triality
I gave a presentation in the Teacher Inquiry class mentioned earlier, where we manipulated Möbius strips. The professor found the idea interesting and used it (with a h/t to me) to illustrate a method of teacher inquiry in the International Encyclopedia of Teacher Education (2022).
Quadrality
This is the reason I am writing this piece. At first, I thought the duality metaphor was the most interesting thing. Then I learned about topology and cutting up the strips. Recently I got out of bed in the middle of the night to see if it was possible to make a Möbius strip out of a square of paper. Common sense told me I couldn’t but then I wondered what if I did it with a square of stretchy fabric or rubber. I went straight to where the experts are always ready to chime in: r/math.
This first answer “You certainly can” came back quickly and made me think, “of course you can!”, but it was then massively downvoted and people generally agreed that it cannot (using a lot of words that were new to me).
In any case, even if it cannot be done in three dimensions, it can surely be done in two dimensions (or four?) so I will ask you to imagine:
- A square, where each edge represents one element of a 4-stage cycle.
- Folding that square to make a Möbius strip: the “stages” are no longer separate – they are integrated into one process with one side. The quadrality is unified and represented as a single iterative process.
╬╬
First, I thought of the Kolb’s Cycle. This works well as it is possible to “begin” this cycle at any stage, though something must have preceded/prompted this beginning so this “Möbius square” essentially represents constructivism.
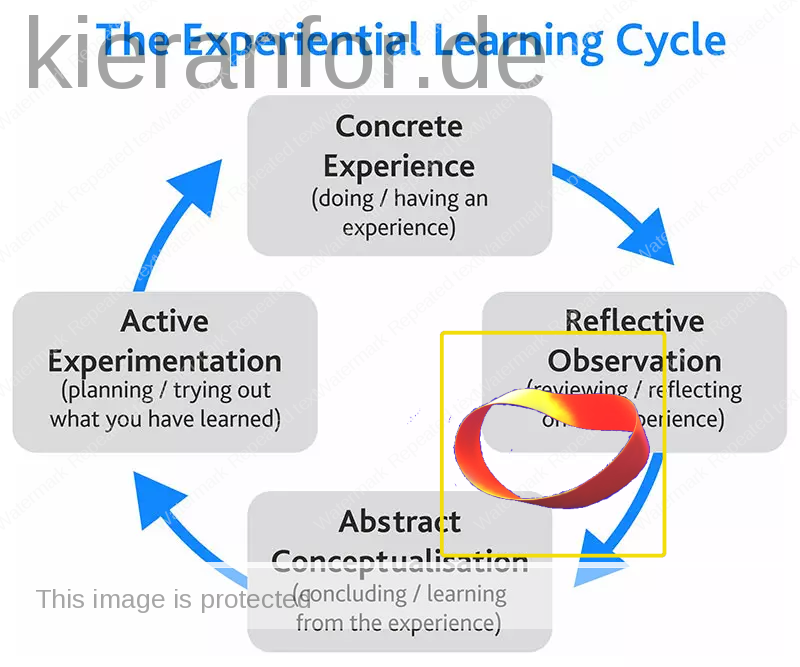
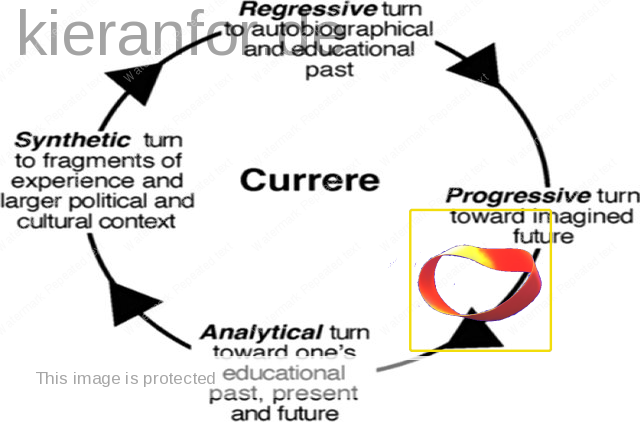
Next, I thought of currere. This process “begins” with reflection, though this reflection takes place in the present perhaps prompted by thoughts of the future so, again, the holistic nature of the representation is helpful. It is not a simple sequence of steps; it is an integrated way of be(com)ing that “hints at the transtemporal and transconceptual” (Pinar, 1975, p. 19).
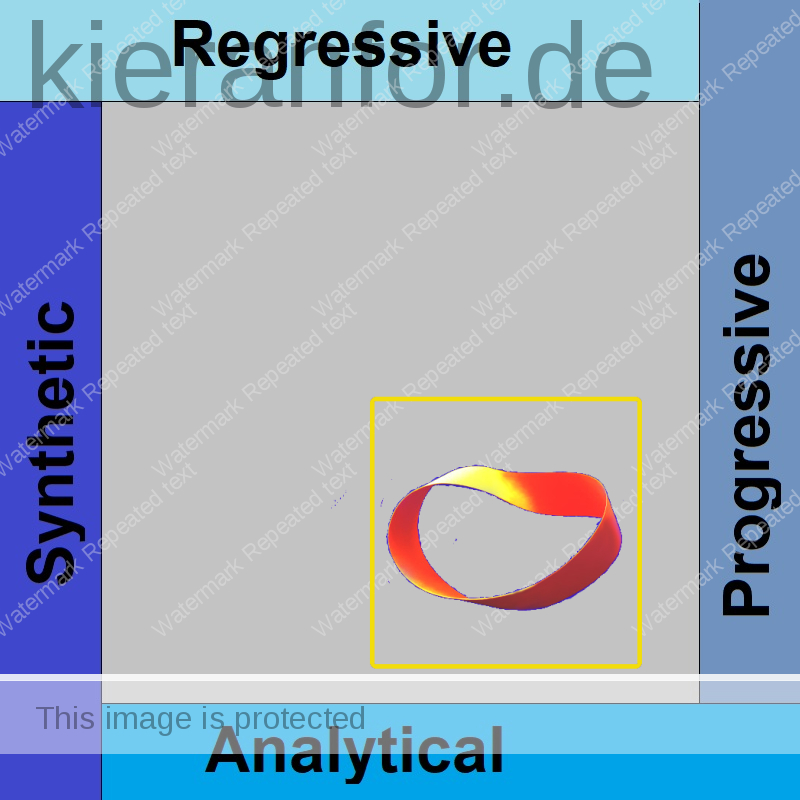

So, this is as far as I have gotten. It is wonderful to have the time and ability to “play gracefully with ideas” like this. I think there is something valuable here but I need to let it rest for now.
Apr 14, 2023: post scriptum
- In communication about the above, Bill Pinar pointed me in the direction of the title below as an introduction to the concept of “ocularcentrism”: it’s certainly worth……eh…a……look? ಠ~ಠ
- Jay, Martin. 1993. Downcast Eyes: The Denigration of Vision in Twentieth-Century French Thought. Berkeley: University of California Press.
Sept 13, 2023
Today, I learned a little about panarchy: “a conceptual framework to account for the dual, and seemingly contradictory, characteristics of all complex systems – stability and change“
This is a note for me to return to this image
https://hackernoon.com/the-adaptive-cycle-panarchy-as-dynamic-maps-for-resilience-thinking-793fad49de5e
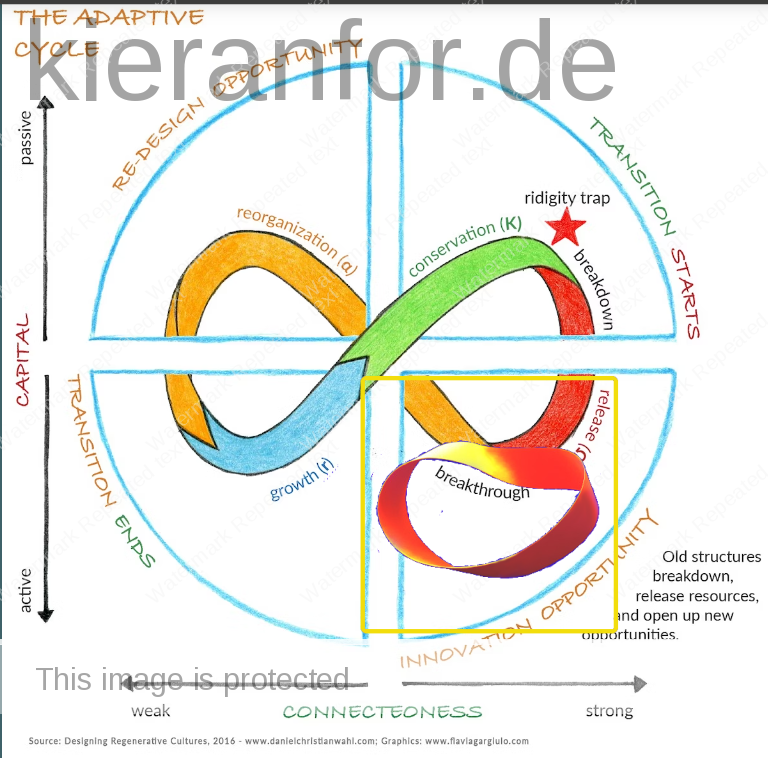

https://www.linkedin.com/pulse/embracing-ouroboros-unraveling-infinite-loop-creativity-duran/
Archive: https://archive.is/HCq94 : https://archive.is/2CreP
∞
Ames Window
Klein Bottle: Cliff Stoll (via Hatch?)